Introducción
En esta unidad continuaremos el estudio de las funciones y en particular las funciones racionales y las funciones con radicales. Se analizará su comportamiento dando relevancia a su dominio, su rango y para las funciones racionales, los puntos de ruptura y además se verificará la relación de dichos puntos con las asíntotas verticales. Para tal efecto iniciamos con el planteamiento de fenómenos en los que se involucran funciones racionales.
Cuando se habla de una modelo matemático para un fenómeno del mundo real, se refiere a una función que describe por lo menos de manera aproximada la dependencia de una cantidad física de otra. Por ejemplo:
- La ley de Boyle dice que cuando una muestra de gas se comprime a una temperatura constante, la presión del gas es inversamente proporcional al volumen del mismo.
- El número de días que se necesitan para completar un trabajo varía inversamente con el número de hombres que trabajan en él, si lo hacen con igual rapidez.
- La base de un triángulo de área constante varía inversamente con su altura.
- El volumen de un gas a temperatura constante varía inversamente con su presión.
- La presión es inversamente proporcional a la altura.
- La temperatura a la que hierve el agua varía inversamente con el número de metros sobre el nivel del mar.
- El monto de capital necesario para producir un ingreso dado varía inversamente con la tasa de interés.
- La fuerza necesaria para levantar una roca varía inversamente con la longitud de la palanca usada.
- La iluminación de un objeto varía inversamente con el cuadrado de la distancia de la fuente luminosa al objeto
- El volumen de un gas varía directamente con la temperatura e inversamente con la presión.
- La resistencia eléctrica de un cable varía directamente con su longitud e inversamente con el cuadrado de su diámetro.
- La ley de gravitación de Newton dice que dos objetos con masas m1 y m2 se atraen entre sí con una fuerza que es conjuntamente proporcional a sus masas e inversamente proporcional al cuadrado de la distancia entre los objetos.
Estos son solo ejemplos de fenómenos del mundo real en los que para construir un modelo matemático que los represente, es necesario hacer uso de las funciones racionales. Para construir la función asociada con cada uno de los fenómenos planteados y muchos otros, resulta útil recordarlo que significa, la variación directa, la variación inversa, la variación conjunta y la variación combinada.
Variación directa: Si
cuando
se dice que y es directamente proporcional con x.
Variación inversa: Si
cuando
se dice que y es inversamente proporcional con x.
Variación conjunta: Si
cuando
se dice que z es conjuntamente proporcional con x y con y.
Variación combinada: Si
cuando
se dice que z es directamente proporcional con x e inversamente proporcional con y.
En todos los casos a la k se le llama constante de variación o constante de proporcionalidad.
Como parte de la introducción se le dará solución al primer problema planteado, en el cuál como se observará es necesario utilizar un modelo en el que se usa una función racional. También algunos de estos fenómenos serán modelados a través de una función, pero antes se trabajarán las generalidades de las funciones racionales, siendo éstas: el dominio, la gráfica y el rango.
Situación que da lugar a una función racional
La ley de Boyle dice que cuando una muestra de gas se comprime a una temperatura constante, la presión del gas es inversamente proporcional al volumen del mismo:
a) De una función que modele la ley de Boyle
b) Construya la gráfica considerando que k=1
c) Que ocurre cuando el volumen aumenta
a) De una función que modele la ley de Boyle
b) Construya la gráfica considerando que k=1
c) Que ocurre cuando el volumen aumenta
Solución:
a) Supongamos que p represente a la presión del gas y que v representa el volumen, ahora si recordamos la variación inversa, obtenemos que:
a) Supongamos que p represente a la presión del gas y que v representa el volumen, ahora si recordamos la variación inversa, obtenemos que:
donde k es la constante de proporcionalidad. A continuación con el fin de manejar la notación de funciones, establecemos las siguientes equivalencias. Supongamos que f(v) representa la presión del gas y que v representa el volumen, luego la función es:
como el volumen no puede ser cero ni negativo, entonces el
b) La gráfica de la función es:
c) En la gráfica observamos que cuando el volumen aumenta la presión del gas disminuye
Gráfica, Dominio y Rango de Funciones Racionales
A continuación se dan las características generales para cada una de estas funciones, se plantean varios ejemplos de funciones racionales en las que se da el dominio, se construye su gráfica y se indica el rango para cada una de ellas y posteriormente se les da solución a algunos de los problemas indicados al inicio de esta sección.
Las funciones racionales son de la forma
en las que p(x) y q(x) son funciones polinomiales, el dominio para estas funciones es
es decir: son todos los números reales excepto los valores de x para los que la función q(x) es cero. El rango de la función Rf es el intervalo que la gráfica cubre sobre el eje Y.
Antes de iniciar los ejemplos continuaremos haciendo uso de las translaciones y rotaciones (c>0) y además se recuerdan:
indica desplazar c unidades la función f(x) hacia arriba.
indica desplazar c unidades la función f(x) hacia abajo.
indica desplazar c unidades la función f(x) hacia la derecha.
indica desplazar c unidades la función f(x) hacia la izquierda.
indica reflejar la función f(x) con respecto al eje X.
indica reflejar la función f(x) con respecto al eje Y.
indica alargar verticalmente la función f(x), por un factor k, alejándose del eje X.
indica contraer verticalmente la función f(x), por un factor k, hacia el eje X.
Material elaborado por los profesores:
Sofía B. E. Salcedo M.
Juan Tamayo Z.
Juan Terrazas C.
Florencio Vera B.
FUNCION RACIONAL
Una función racional es el cociente de dos funciones, p(x) y q(x)
donde p(x) y q(x) son funciones polinomiales y q(x) es una función diferente de cero; es decir,
 Tratemos de relacionar que este es un "modelo general", vamos a ubicarnos en el denominador, ya que es la parte que nos interesa para obtener el dominio de esta función. Ahora bien, si el denominador lo igualas a cero, significa que debemos escribir q(x)=0, es decir si queremos saber el valor de x, cuando este se hace cero, escribirmos x-2=0, haciendo las operaciones de despeje que ya utilizas tienes que x=2, con este valor decimos: el dominio de la función (de arriba) son todos los reales excepto el dos, representado de la siguiente manera:
Tratemos de relacionar que este es un "modelo general", vamos a ubicarnos en el denominador, ya que es la parte que nos interesa para obtener el dominio de esta función. Ahora bien, si el denominador lo igualas a cero, significa que debemos escribir q(x)=0, es decir si queremos saber el valor de x, cuando este se hace cero, escribirmos x-2=0, haciendo las operaciones de despeje que ya utilizas tienes que x=2, con este valor decimos: el dominio de la función (de arriba) son todos los reales excepto el dos, representado de la siguiente manera:
Observa que si alejamos nuestro zoom, del area de la gráfica, (observa la escala) ¿que sucede con las ramas de la función?
¿Como obtendrías el dominio a partir de la gráfica?
El dominio son todos los reales excepto donde pierde continuidad la gráfica (o se corta la gráfica) en los valores x=2,-2. Que se escribe de la siguiente manera:
Comenzando una pequeña prueba para enlazar un applet de geogebra y puedas analizar la función radical en cuanto a sus desplazamientos.
Una función racional es el cociente de dos funciones, p(x) y q(x)
Esto significa que todos aquellos valores de x que hagan posible que q(x)=0 no serán parte del dominio. Por ello, se dice que el dominio de una función racional es el conjunto de todos los números reales con excepción de aquellos valores que permitan que q(x)=0.
Estos son algunos ejemplos de funciones racionales:
Dominio, Rango y asíntotas de una función racional
Para determinar el dominio de una función racional, creo que podrás entenderlo con un ejemplo. Veamos:
Ejemplo 1.
Determina el dominio de la función
Solución: Recuerda que el dominio de una función racional se caracteriza por ser el conjunto de todos los reales con excepción de aquellos valores que hagan cero a la función q(x), es decir el denominador.
 Tratemos de relacionar que este es un "modelo general", vamos a ubicarnos en el denominador, ya que es la parte que nos interesa para obtener el dominio de esta función. Ahora bien, si el denominador lo igualas a cero, significa que debemos escribir q(x)=0, es decir si queremos saber el valor de x, cuando este se hace cero, escribirmos x-2=0, haciendo las operaciones de despeje que ya utilizas tienes que x=2, con este valor decimos: el dominio de la función (de arriba) son todos los reales excepto el dos, representado de la siguiente manera:
Tratemos de relacionar que este es un "modelo general", vamos a ubicarnos en el denominador, ya que es la parte que nos interesa para obtener el dominio de esta función. Ahora bien, si el denominador lo igualas a cero, significa que debemos escribir q(x)=0, es decir si queremos saber el valor de x, cuando este se hace cero, escribirmos x-2=0, haciendo las operaciones de despeje que ya utilizas tienes que x=2, con este valor decimos: el dominio de la función (de arriba) son todos los reales excepto el dos, representado de la siguiente manera: ¿Como sería la gráfica?
¿Donde está ubicado x=2?
Está puntueado porque no siempre se dibuja, esto te debe de ayudar para que analices como se comportan las ramas de la gráfica,
Observa que si alejamos nuestro zoom, del area de la gráfica, (observa la escala) ¿que sucede con las ramas de la función?
Pareciera que se juntan las ramas negras con la roja punteada, y las otras se juntan con el eje x.
¿crees que la rama que estan sobre el eje x llegan realmente a juntarse?
Para verificar esto puedes dar valores a la función es decir que x=1000000
la función evaluada en 1000000 da como resultado 0.000003, (y=0.000003)
Se va acercando al cero pero no es CERO.
Prueba evaluando con más valores y comprueba que la rama nunca va a tocar al eje x.
Si avanzas por la gráfica, sobre el eje x de izquierda a derecha, la rama se sube y la otra viene de abajo hacia arriba y gira hacia la derecha.
Ubiquemonos en las que estan verticales.
La recta x=2 (linea vertical roja punteada o discontinua), será nuestro parteaguas.
El dominio son todos los reales excepto donde se hace cero el denominador de la función.
Veamos otro ejemplo
Ejemplo 2:
Determina el dominio de la función:
Solución:
El denominador es
que igualaremos a cero:
despejando a x obtenemos dos valores:
¿que significan estos valores?
Observa la gráfica:
Alejando un poco el zoom de la gráfica (observa la escala)
¿crees que la rama que estan sobre el eje x llegan realmente a juntarse?
Para verificar esto puedes dar valores a la función es decir que x=1000000
la función evaluada en 1000000 da como resultado 0.000003, (y=0.000003)
Se va acercando al cero pero no es CERO.
Prueba evaluando con más valores y comprueba que la rama nunca va a tocar al eje x.
Si avanzas por la gráfica, sobre el eje x de izquierda a derecha, la rama se sube y la otra viene de abajo hacia arriba y gira hacia la derecha.
Ubiquemonos en las que estan verticales.
La recta x=2 (linea vertical roja punteada o discontinua), será nuestro parteaguas.
El dominio son todos los reales excepto donde se hace cero el denominador de la función.
Veamos otro ejemplo
Ejemplo 2:
Determina el dominio de la función:
Solución:
El denominador es
que igualaremos a cero:
despejando a x obtenemos dos valores:
¿que significan estos valores?
Observa la gráfica:
Alejando un poco el zoom de la gráfica (observa la escala)
¿Como obtendrías el dominio a partir de la gráfica?
El dominio son todos los reales excepto donde pierde continuidad la gráfica (o se corta la gráfica) en los valores x=2,-2. Que se escribe de la siguiente manera:
Funciones con Radicales






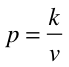































muy bueno!! muchas gracias por el tutorial
ResponderEliminarMuy buen aporte le entendí bastante
ResponderEliminar